Nouvelles méthodologies en géostatistique
Simulations de champ gaussiens sur la sphère
Des covariances différentes conduisent a des textures fortement indifférenciées. En particulier, la covariance linéaire crée des anti-corrélations qui se manifestent par un effet jour-nuit sur la réalisation. Ces simulations sur la sphère sont utilisées notamment pour modéliser les phénomènes climatologiques au niveau du globe terrestre.
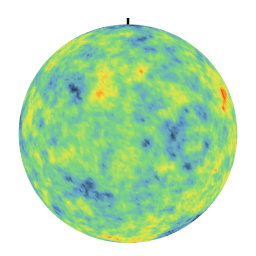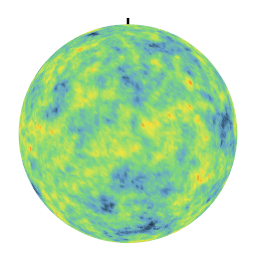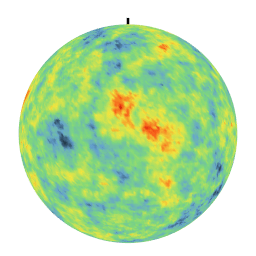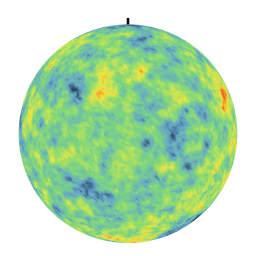 |  |
| Covariance exponentielle | Covariance linéaire sur [0,pi] |
Géostatistique par l'approche SPDE
De nombreux verrous opérationnels de la Géostatistique sont levés en utilisant le fait que les fonctions aléatoires peuvent être vues comme solutions d'équations aux dérivées partielles stochastiques (EDPS).
La résolution numérique de ces équations (éléments finis) ouvre la voie à une géostatistique plus efficace car basée sur des matrices creuses.
Par ailleurs, en rendant les coefficients des EDPS variables dans l'espace, cela permet de s'affranchir des hypothèses de stationnarité des structures (ex: anisotropie variable)
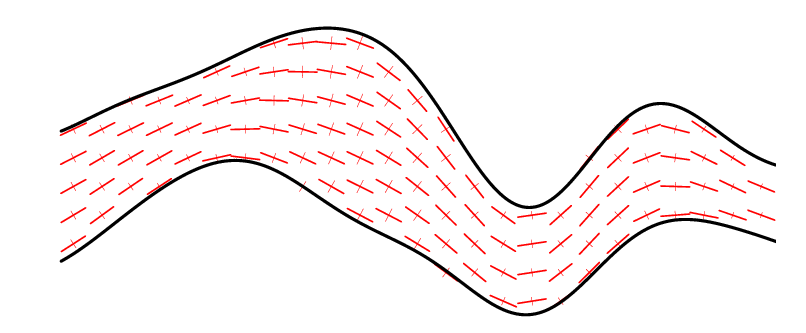 | 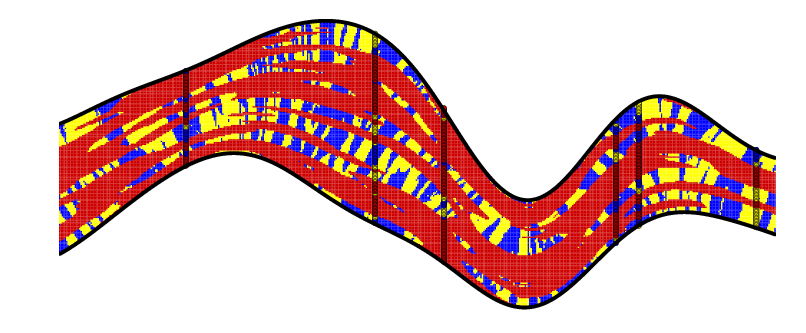 |
| Anisotropie qui suit la géométrie de la couche | Réalisation d'une fonction aléatoire Plurigaussienne conditionnée par les faciès échantillonnés le long de 5 sondages verticaux. |
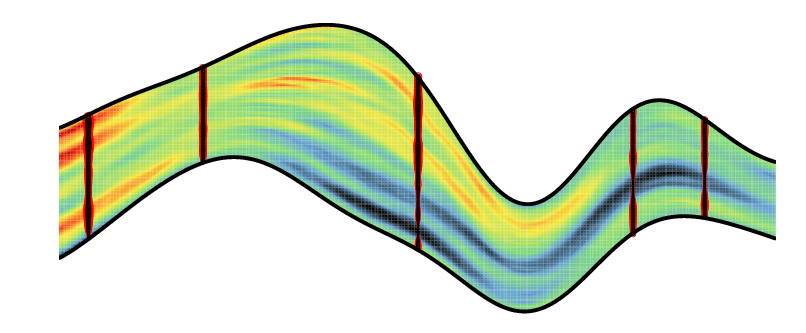 | 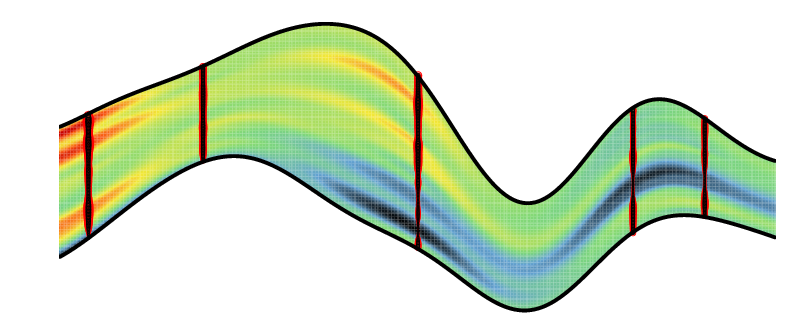 |
| Simulation d'une variable gaussienne conditionnée par des données échantillonnées le long de 5 sondages verticaux. | Estimation par krigeage d'une variable gaussienne conditionnée par des données échantillonnées le long de 5 sondages verticaux |
Le modèle SPDE permet de prendre en compte des anisotropies complexes, en particulier non dépliables (exemple du vortex)
 | 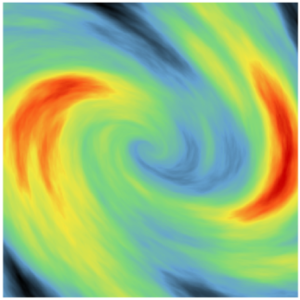 |
| Champ d'anisotropie | Simulation SPDE avec anisotropies complexes |
L'extension à une variété Riemannienne régulière est immédiate dès lors que son maillage est disponible.
 | 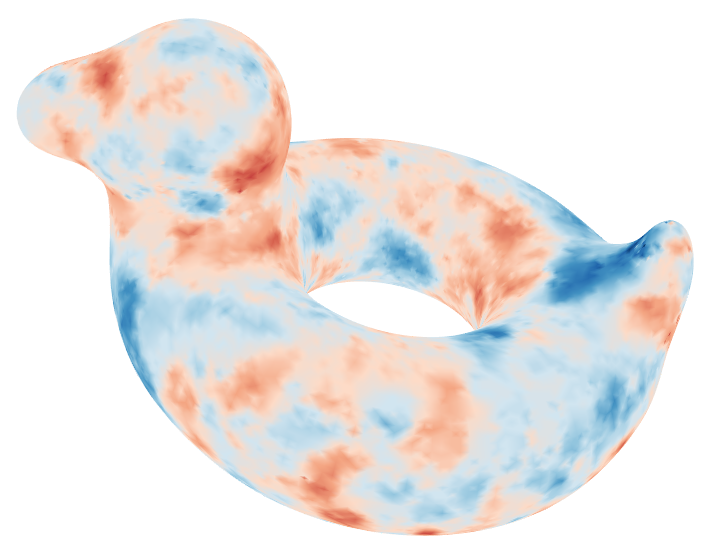 | 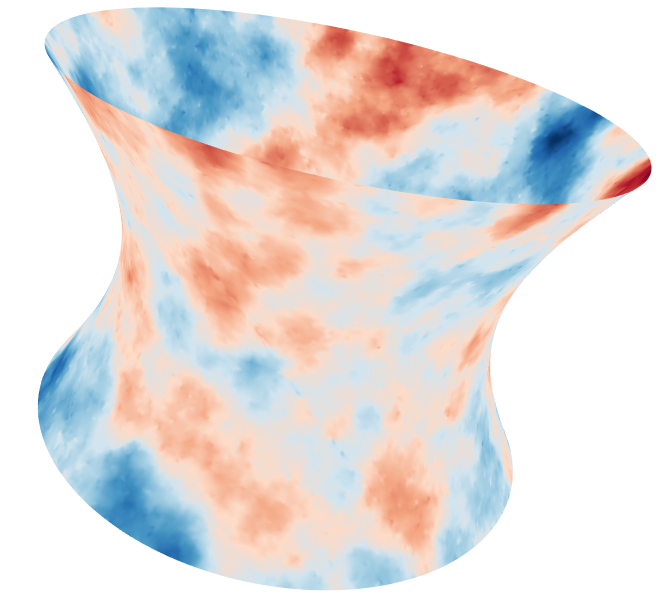 |  |
| Simulations gaussiennes | Simulation gaussienne seuillée | ||
Modèles SPDE spatio-temporels
L'approche SPDE se décline aussi pour la modélisation des phénomènes spatio-temporels.
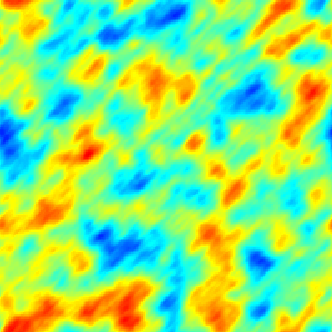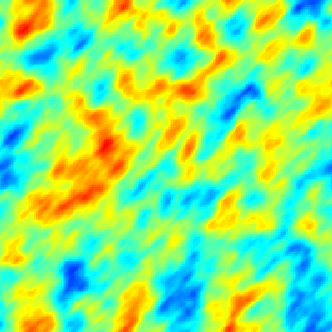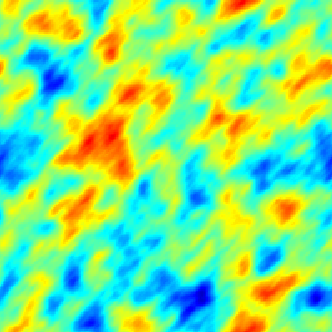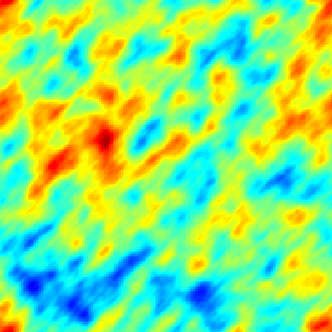 | 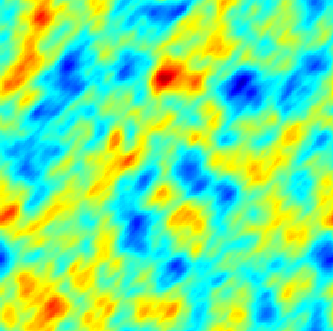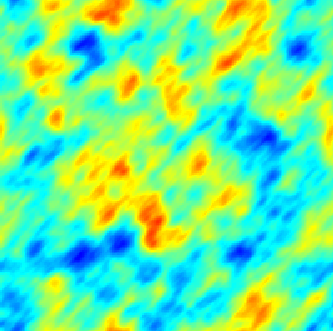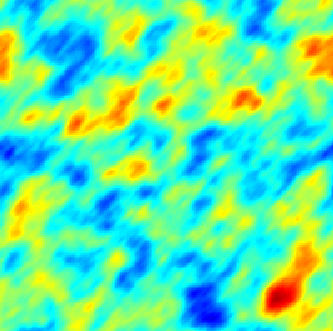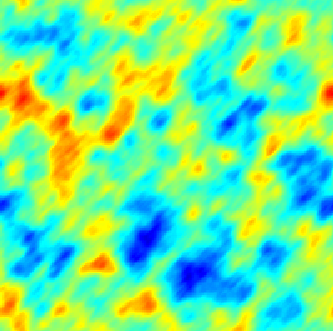 | 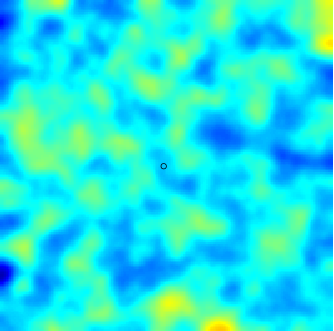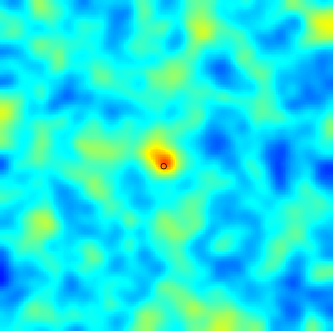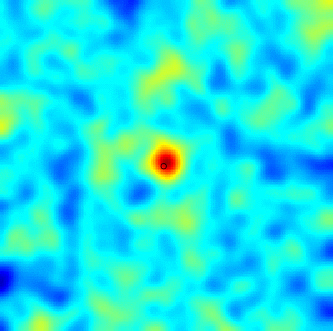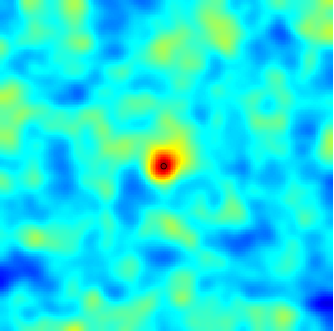 |
| Modèle séparable (espace-temps) | Avec advection | Modèle diffusif avec termes sources (déterministe + aléatoires) |
Dans le cadre spatio-temporel, l'approche SPDE permet d’intégrer des comportements dictés par les processus physiques (diffusion, advection, ...) aux modèles géostatistiques.
Modèle max-stable
Champ aléatoire extrémal gaussien : obtenu comme le maximum de champs aléatoires gaussiens (de covariance donnée) pondérés par des temps d’arrivée de processus de Poisson. Ces modèles sont aptes à représenter des phénomènes spatiaux présentant des valeurs extrêmes. Ils sont utilisés pour représenter des champs de températures ou de pluviométrie dans des circonstances exceptionnelles (ex: épisodes cévenoles)
 | 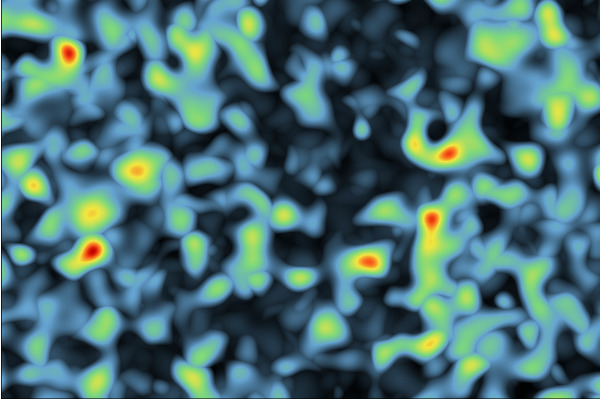 |
| Covariance exponentielle | Covariance gaussienne |
Modèle de fonctions aléatoires de substitution
Le modèle de fonction de substitution repose sur la combinaison d'une fonction aléatoire spatialisée et d'un processus de codage. Il permet de réaliser des simulations conditionnées par des données de faciès. Ce modèle a été appliqué avec succès pour reproduire la géométrie et la morphologie des stromatolites dans le cadre d'une étude réalisée au profit d'une société pétrolière internationale.
 | 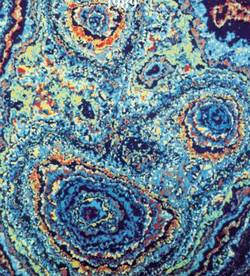 | |
| Stromatolite coll. Géologie © J.-Y. Reynaud, MNHN | Simulation d'une fonction de substitution (fonction directrice de Chentsov, fonction de codage markovienne à loi stationnaire uniforme) |
